Expressions allow to use mathematical formulas to be used in d3web knowledge bases. In every formula you may access existing questions and their values, as well as predefined constants. The results of those formulas may be used to assign it to an existing question (e.g. in a rule action) or as a condition in a rule.
This tutorial is built in three chapters:
- The supported markups and how expression can be used there.
- The expression syntax with detailed information on the expression's capabilities.
- A function reference table with a list of all available functions and their documentation.
Supported Markups#
The expressions are integrated in a bunch of existing markups, as well as defining some additional markups.
Rules#
Expression can be used in %%Rule markup in both conditions and actions. In both, it must be surrounded by eval(...) containing the expression. When using the expression as a condition, the expression must result to a boolean value, otherwise an error is signaled and the rule will not be created. The rule will fire if the condition evaluates to "true". In the following example the rule will fire of the gradient of question "measurement" is above 1 during the last 10 seconds.
%%Rule IF eval(gradient(measurement[-10s, 0s]) > 1) THEN ... %
For rule actions the expression can be used to assign the resulting value to an abstract question. The expression is also surrounded by eval(...), preceded by the question to be assigned. Please note that the questions type must be compatible to the result of the expression, otherwise an error is signaled and the rule will not be created. In the following example the question myGradient will be assigned to the gradient, the question "measurement" had during the last 10 seconds:
%%Rule IF measurement = known THEN myGradient = eval(gradient(measurement[-10s, 0s]) ) %
Direct question assignment#
Using the markup %%Variable you can directly assign the result of an expression to an existing question. Please note that the questions type must be compatible to the result of the expression, otherwise an error is signaled and the assignment will not be created. Unlike using the expressions in rules, no eval(...) is required. The assignment is always kept up-to-date, so the value of the assigned question is never outdated.
%%Variable myGradient = gradient( measurement[-10s,0s] )
Defining Constants#
Constants are helpful to define values that have a special meaning and therefore naming it. Those constants can be of any type (e.g. number, date, boolean) and can be used in any expression instead the direct value. This gives you the possibility to also alter the constant's value in the wiki without altering all the usages of the value.
Defining a constant is identical to defining a direct question assignment, but instead of a predefined question the constant name is to be written left to the expression. The type of the constant is automatically derived by the result of the expression. Note that defining a constant, neither questions nor other constants are allowed to be used in the defining expression. See some examples:
// define a numeric constant %%Constant pi = 3.14159265358979323846 // define a date constant (see special date notation) %%Constant bostonTeaParty = #1773-12-16# // you may also use operators and functions %%Constant silvesterParty = #1999-12-31# + 19h + 30min %%Constant pi_of_Archimedes = 3 + 9552/67441 // using other constants is NOT ALLOWED!!! --> error signaled %%Constant invalidDeclaration = 2*pi
Flowcharts#
Expressions can also be used in the flowchart graphical editor. Similar to rules the expressions can be used as both assignments in nodes and conditions on arrows.
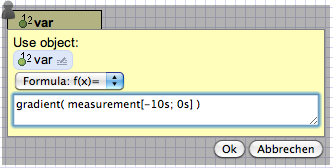 |
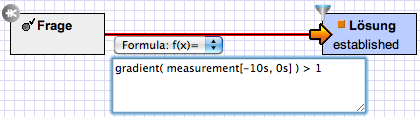 |
Expression syntax#
Basic calculations#
You can write expression in a natural operator infix-notation. For mathematical calculations you can use the common operators "+", "-", "*", "/" to addition, subtraction, multiplication and division. In addition the infix operator "^" for power is also defined. The operators have their priority as usual in algebra (1: "^"; 2: "*", "/"; 3: "+", "-"). Brackets can be used to change priority of evaluation.
// examples of valid expressions 1 + 3 // result is 4 2 ^ 16 - 1 // result is 65635 2 ^ (16 - 1) // result is 32768
Types and literals#
Each element in an expression has a defined result type. The following types are defined: numbers, booleans, durations, time-points and strings. In the examples above, only numbers are used. By typing a number in an expression you have defined a literal constant. But also the other types have their literal constants to be used in expressions:
| Type | Syntax | Description / Example |
|---|---|---|
| Number | <DD> <DD>.<DD> <DD>.<DD>e+-<DD> | <DD> is any number character sequence. Defines a number literal constant, either an integer number or an rational number or a floating point number in exponent notation. Examples are "12" or "125.17" or "1.1e-23". |
| Boolean | "true" "false" | Defines a boolean literal constant either being true or false. |
| Duration | <NUMBER>"ms" <NUMBER>"s" or "sec" <NUMBER>"min" <NUMBER>"h" <NUMBER>"d" | <NUMBER> is a number literal constant as described above. It is appended by a duration unit which may be "ms" for milliseconds, "s" or "sec" for seconds, "min" for minutes, "h" for "hours" or "d" for days. Examples are "1.5d" for 36 hours of time or "1s" for one second. |
| Time-Point | #YYYY-MM-DD# | Defines a date as a time-point, where "YYYY" is the year, "MM" is the month (1-12) and "DD" is the day of the month. The time-point literal is always at 0:00 o'clock of the specified date. If a special time is meant, simply add a duration to the date. Examples are "#2000-01-01#" for the millenium sylvester and "#1999-12-31# + 19h" for the party starting at 7pm the day before. |
| String | '<any_characters_here>' | Defines a string literal constant. Please note the single quotes to be used for string literals. If the string shall contain a single quote character use "\'" inside the string literal. Examples are "'my string'" or "'quote means \' here'". |
For each type there is also a history of that type available. A history is the evolution of a single value over a certain range in time. A history consists of a sequence of past values. Each value is associated with a time-point when the value has been set. For a history, each value is assumed to be valid from its time-point until the next value of the history has been set.
Boolean expressions#
For comparing values the operators "=" (or "==", which is identical), "<", "<=", ">", ">=" and "!=" are defined. The result of these compare operators are a boolean value, "true" or "false" to be more precise. For booleans there are also some additional infix operators defined: "&" for "logical and" and "|" for "logical or", as well as "&&" and "||" which are identical to "&" and "|". You can also use "!" for logical negation.
// example comparators 1 >= 3 // true 2^16-1 == 65535 // true // example boolean operators true & false // false true | false // true true & !false // true
Using functions#
There are a lot of functions provided, that can be applied to a set of arguments. See function reference table for a complete set of all available functions. Each function has a number of signatures describing the arguments allowed to be used for the function.
A function is called by writing the function name followed by brackets. Inside the brackets the arguments of the function can be listed, separated by ",". Examples of functions are:
floor( 3.23 ) // results to 3 average( 1, 2, 3, 4 ) // results to 2.5
Each of the infix operators available have also a corresponding function. By looking in the function reference table you can see to what argument types the operators can be applied to.
| Operator | Function | Desciption |
|---|---|---|
| ^ | pow | Returns the value of the first argument raised to the power of the second argument. |
| * | mult | Returns the product of the two arguments. |
| / | div | Returns the ratio of the two arguments. |
| + | plus | Returns the sum of the two arguments. |
| - | minus | Returns the difference of the two arguments. |
| ! | not | Returns true, if the argument is false, and vica verse. |
| &, && | and | Returns false, if one argument is false. |
| |, || | or | Returns true, if one argument is true. |
| =, == | equal | Returns true, if both argument are equal, false otherwise. |
| != | unequal | Returns true, if both argument are not equal, false otherwise. |
| < | lt | Returns true, if the first argument is less than the second one, false otherwise. |
| <= | le | Returns true, if the first argument is less or equal than the second one, false otherwise. |
| > | gt | Returns true, if the first argument is greater than the second one, false otherwise. |
| >= | ge | Returns true, if the first argument is greater or equal than the second one, false otherwise. |
| [] | -- | Access the full history to a certain question. This operator has no functional equivalent. |
| [...] | valueAt | Access a value of a history to a certain time. |
| [..., ...] | subHistory | Access a sub-history in a certain time range. If there is not value directly at the start of the subhistory, the next earlier value will be included. |
| ![..., ...] | strictSubHistory | Access a sub-history in a certain time range. The sub-history will not contain values that were set before the given start. |
Access question and solution values#
You can access the current value of a question by simply writing the question's or solution's name in a formula. If the name contains any non-alphanumeric characters, you can use double quotes on the name. Referring to a question or solution, the current (most recent) value is used when the expression is evaluated.
// access question values
floor(myQuestion + 1) // using the current value of myQuestion
floor("My special question" + 1) // using the current value of the question "My special question"
Using questions or solutions, you can also use the special []-operator, that allows you to access a past value of the object or it's whole history. Please note that this is only allowed for questions and solutions that are recorded in the time database. This is the default behaviour, but may be altered setting the object's property "history" to "false". The []-operator has different possible usages:
- <object-name>[]:
Returns the whole history of the object with the name <object-name>. It contains every known value of the object since the session has been started. - <object-name>[<time-point>]:
Returns the value of the object with the name <object-name> that has been valid for the specified <time-point>. If the object has not been set to that time-point, the most recent value before that time will be used. If the object had not been set at all till the specified time, "undefined" is returned. - <object-name>[<time-point>, <time-point>]:
Returns the sub-history of the object with the name <object-name> starting from the earlier of the two time-points and lasting to the latter one. The sub-history contains all values of the object's full history that have been valid during the specified interval. This lead to that the sub-history usually starts before the specified time-points and have their latest value before the latter of those specified time-points. - <object-name>![<time-point>, <time-point>]:
Returns the strict sub-history of the object with the name <object-name> starting from the earlier of the two time-points and lasting to the latter one. The sub-history contains all values of the object's full history that have been set during the specified interval. In contrast to the 'normal' sub-history, this strict sub-history will not maybe start before the specified earlier time-point, but only at that earlier time-point or later (but of course not later than the later time-point).
// access question values myQuestion[now - 10min] // using the value of myQuestion 10 minutes ago // access question histories average(myQuestion[]) // average of all values myQuestion had before (incl. current one) average(myQuestion[now-10min, now]) // average of the last 10 minutes average(myQuestion![now-10min, now]) // average of all values that were set between 10 minutes ago and now
Instead of using time-points, the operator also allows to use durations (e.g. "10min"). Using a duration means that you refer to the time the specified duration ago. Regardless to whether the duration is positive or negative, the operator always goes into the past starting at the "recent time". This "recent time" is the latest time the object has been set, but not from the global variable 'now'. Especially for rarely set objects this can make a big difference.
// using durations instead of time-points myQuestion[10min] // using the value of myQuestion 10 minutes before its latest value average(myQuestion[-10min, 0min]) // average of the last 10 minutes since the latest value average(myQuestion[10min, 0min]) // identical to the line above
Using questions in formulas, the questions will be interpreted as following:
- [num]: Number
- [yn]: Boolean
- [oc]: Number (Its value is a natural/integer number, starting at 1 for the first choice, 2 for the second one and so on.)
- [mc]: -- (These questions are not allowed to be used in expressions, since no appropriate interpretation can be defined.)
- [date]: Time-Point
- [text]: String
Using solutions in formulas the solution's value is a numeric integer value as following:
- EXCLUDED: 0
- UNCLEAR: 1
- SUGGESTED: 2
- ESTABLISHED: 3
Access question choices#
You can also access the choices of the questions as constant symbols. The choices have their value defined by "1" for the first choice of a question, "2" for the second one, and so on. Since the name of choices are not unique, but identical named choices may have different values for different question, it is necessary to link the choice to the correct question.
Usually in expression you can simply write the choice, after you have used the question before. To have this simple rule, there is complex identification behind, you usually not get noticed of. Here it is how the choices are matched to their choice-questions (both, [oc] and [yn]):
- If you use a choice-question in a function call, its choices are known in every following argument of that function. Thus in "equal(myQuestion, ...)", the choices of myQuestion are known at the second argument.
- If multiple questions are used all choices of all questions are known to the following arguments. Thus in "average(myQuestion1, myQuestion2, ...)" the third argument can refer to choices of both questions.
- Choices does not overwrite other literal symbols. Choices of questions will not be overwritten by the following question's choices.
- If a question is used in a sub-expression, being a functions argument, the choices of the question are also known at the following arguments of the function, if the sub-expression's result "still refers to the choice-question". This is a complex thing, so see the example "equal(max(myQuestion), myChoice)". Here the function max still refers the to values of myQuestion, thus myChoice can be used to refer to a choice of myQuestion. In contrast, "equal(gradient(myQuestion), myChoice)" will fail, because the gradient has a complete different meaning.
- Infix-operators are treated exactly as their functional notation. Thus "question = foo" is identical to "equal(question, foo)".
As mentioned you usually not in charge to be aware of this rule. Simply use choices natural to after their questions:
myQuestion[-10s] = myChoice myQuestion = myChoice && myOtherQuestion = myOtherChoice average( myQuestion[] ) > myChoice
You can also directly refer to any choice of any question, under ignorance of all the rules above. To do that simply use the question name, append "#" and the choice name. If the question or choice contains any special characters or white-spaces use double quotes around the whole literal:
// direct access to choices myQuestion#myChoice "My special question#my special choice"
Access solution states#
You can also access the states of a solution as constant symbols, similar to question choices. The states have their value defined by "0" if the solution is excluded, "1" for neutral, "2" for suggested and "3" for established solutions. Usually the rating states for a certain solution can be accessed by their name (e.g. "ESTABLISHED"). The behavior is identical to choice questions, thus refer to the section above for more details.
mySolution[-10s] = ESTABLISHED median( mySolution[] ) >= SUGGESTED
Special keywords#
There is also a number of special literal tokens defined when using expression. Those tokens are:
- start: time-point representing the start of the d3web-session. It will be initialized once and never be changed during the session. Please note that the start time is not tied to the system's clock, it might differ from that.
- now: time-point representing the most recent time of the d3web-session. It will update frequently, every time any value is set at a newer time or if the time database is explicitly told to proceed in time. Please note that the now time is not tied to the system's clock, it might differ from that.
- true, false: boolean literals for the true and false value
- pi: the value of pi, defined as 3.141592653589793
- e: the value of e, defined as 2.718281828459045
Undefined values#
When using questions in expressions, their values may be undefined, e.g. no value has been set to the question. In addition also functions may return undefined, e.g. calculating the average of an empty history. Most functions will return undefined if any of it's arguments is undefined. Otherwise, function's behavior on undefined values is denoted by the individual functions.
Function Reference#
Below you see all functions that come with the TimeDB plugin by default. If you need additional functionality that is not covered by the provided functions, you might consider defining your own specialized function using Javascript. See Doc Javascript Functions for more info.
| Function | Documentation |
|---|---|
| [] | Internal function. |
| abs | Returns the absolute value of a double value. |
| acos | Returns the arc cosine of a value; the returned angle is in therange 0. |
| and | Returns false, if one argument is false. |
| asin | Returns the arc sine of a value; the returned angle is in therange -pi/2 through pi/2. |
| atan | Returns the arc tangent of a value; the returned angle is in therange -pi/2 through pi/2. |
| average | Returns the average (mean) value of the one argument history or the set of the argument values. |
| cbrt | Returns the cube root of a double value. |
| ceil | Returns the smallest (closest to negative infinity) double value that is greater than or equal to the argument and is equal to a mathematical integer. |
| cos | Returns the trigonometric cosine of an angle. |
| cosh | Returns the hyperbolic cosine of a double value. |
| count | Returns the number of entries of the argument history. |
| date | Creates a new date with the specified YEAR, MONTH and DAY. |
| dayOfMonth | Returns the day within the month specified by the given date, a value between 1 to 31 (or 30, 28, 29 respectively). |
| dayOfWeek | Returns the day of week of the specified date as integer representation. |
| daysOfMonth | Returns the last day of the month that contains the specified date, so it is either 28 or 29 for february or 30 or 31 for all other months. |
| delta | Returns the difference between the maximum value and the minimum value of the one argument history or the set of the argument values. |
| div | Returns the ratio of the two arguments. |
| duration | Returns the total duration of all entries of the argument history. |
| equal | Returns true, if both argument are equal, false otherwise. |
| exp | Returns Euler's number e raised to the power of adouble value. |
| expm1 | Returns e x -1. |
| filter | Returns a new history with all the values of the given history that do not satisfy the given value or condition (combination of operator and value) being removed. |
| firstChange | Returns the date when the first value of the specified history has been set. |
| floor | Returns the largest (closest to positive infinity) double value that is less than or equal to the argument and is equal to a mathematical integer. |
| ge | Returns true, if the first argument is greater or equal than the second one, false otherwise. |
| gradient | Returns the total increase of a linear fitted line within the given (sub-)history. |
| gt | Returns true, if the first argument is greater than the second one, false otherwise. |
| hour | Returns the hour of a given date. |
| if | Checks the first argument as the condition and returns one of the following arguments as the result of the if-function. |
| invalidCount | Returns the number of invalid entries of the argument history. |
| invalidDuration | Returns the total duration of the invalid entries of the argument history. |
| invalidDurationRatio | Returns the ratio of invalid entrys' durations of the argument history compared to the total duration of all its entries. |
| invalidRatio | Returns the ratio of invalid entries of the argument history compared to the number of its total entries. |
| isNewer | Returns 'lastChange' of the first history is newer as the 'lastChange' time of the second history. |
| known | Checks if the specified value is valid (known). |
| latestChange | Returns the date when the most recent value of the specified history has been set. |
| latestValue | Returns the most recent value stored in the specified history or histories. |
| le | Returns true, if the first argument is less or equal than the second one, false otherwise. |
| log | Returns the natural logarithm (base e) of a double value. |
| log10 | Returns the base 10 logarithm of a double value. |
| log1p | Returns the natural logarithm of the sum of the argument and 1. |
| lt | Returns true, if the first argument is less than the second one, false otherwise. |
| max | Returns the maximum value of the one argument history or the set of the argument values. |
| median | This is an implementation of the median function. |
| min | Returns the minimum value of the one argument history or the set of the argument values. |
| minus | Returns the difference of the two arguments. |
| minute | Returns the minute of a given date, from 0 to 59. |
| mod | Returns the remainder of the of the two arguments. |
| month | Returns the month as a number for a given date, i. |
| mult | Returns the product of the two arguments. |
| neg | Returns the negated value of the argument. |
| not | Returns true, if the argument is false, and vica verse. |
| or | Returns true, if one argument is true. |
| percentEqual | Returns the percentage (between 0 - 1) of the time the specified history has been equal to the specified value. |
| percentGe | Returns the percentage (between 0 - 1) of the time the specified history has been greater or equal than the specified value. |
| percentGt | Returns the percentage (between 0 - 1) of the time the specified history has been less than the specified value. |
| percentIn | Returns the percentage (between 0 - 1) of the time the specified history has been in between the specified min and max value (limits included). |
| percentLe | Returns the percentage (between 0 - 1) of the time the specified history has been less or equal than the specified value. |
| percentLt | Returns the percentage (between 0 - 1) of the time the specified history has been greater than the specified value. |
| percentUnequal | Returns the percentage (between 0 - 1) of the time the specified history has been different to the specified value. |
| plus | Returns the sum of the two arguments. |
| pow | Returns the value of the first argument raised to the power of the second argument. |
| rint | Returns the double value that is closest in value to the argument and is equal to a mathematical integer. |
| round | Returns the closest int to the argument. |
| second | Returns the second of a given date, from 0 to 59. |
| signum | Returns the signum function of the argument; zero if the argument is zero, 1. |
| sin | Returns the trigonometric sine of an angle. |
| since | Returns the date since the value of the specified history remains unchanged. |
| sinh | Returns the hyperbolic sine of a double value. |
| sqrt | Returns the correctly rounded positive square root of a double value. |
| strictSubHistory | Access a sub-history in a certain time range. |
| subHistory | Access a sub-history in a certain time range. |
| tan | Returns the trigonometric tangent of an angle. |
| tanh | Returns the hyperbolic tangent of a double value. |
| toDegrees | Converts an angle measured in radians to an approximatelyequivalent angle measured in degrees. |
| toRadians | Converts an angle measured in degrees to an approximatelyequivalent angle measured in radians. |
| unequal | Returns true, if both argument are not equal, false otherwise. |
| validCount | Returns the number of valid entries of the argument history. |
| validDuration | Returns the total duration of the valid entries of the argument history. |
| validDurationRatio | Returns the ratio of valid entrys' durations of the argument history compared to the total duration of all its entries. |
| validRatio | Returns the ratio of valid entries of the argument history compared to the number of its total entries. |
| valids | Removes all invalid values from the history. |
| valueAt | Access a value of a history to a certain time. |
| year | Returns the year of a given date. |
[]#
Usage: [](«HISTORY»)(Implemented in cc.d3web.expression.eval.FullHistoryFunction)
HISTORY_BOOLEAN -> HISTORY_BOOLEAN HISTORY_DATE -> HISTORY_DATE HISTORY_DURATION -> HISTORY_DURATION HISTORY_NUMBER -> HISTORY_NUMBER HISTORY_STRING -> HISTORY_STRING
Internal function. Returns the specified history as it is.
abs#
Usage: abs(«NUMBER»)(Implemented in cc.d3web.expression.eval.UnaryMathFunction)
NUMBER -> NUMBER DURATION -> DURATION
Returns the absolute value of a double value. If the argument is not negative, the argument is returned. If the argument is negative, the negation of the argument is returned. Special cases:
- If the argument is positive zero or negative zero, the result is positive zero.
- If the argument is infinite, the result is positive infinity.
- If the argument is NaN, the result is NaN.
Double.longBitsToDouble((Double.doubleToLongBits(a)<<1)>>>1)
acos#
Usage: acos(«NUMBER»)(Implemented in cc.d3web.expression.eval.UnaryMathFunction)
NUMBER -> NUMBER
Returns the arc cosine of a value; the returned angle is in therange 0.0 through pi. Special case:
- If the argument is NaN or its absolute value is greater than 1, then the result is NaN.
The computed result must be within 1 ulp of the exact result.Results must be semi-monotonic.
and#
Usage: and(«BOOLEAN», «BOOLEAN»)(Implemented in cc.d3web.expression.eval.LogicalOperator)
BOOLEAN x BOOLEAN -> BOOLEAN
Returns false, if one argument is false. Returns true, if both arguments are true. Otherwise it returns undefined. Instead of the function you can also use the inline operator '&'.
asin#
Usage: asin(«NUMBER»)(Implemented in cc.d3web.expression.eval.UnaryMathFunction)
NUMBER -> NUMBER
Returns the arc sine of a value; the returned angle is in therange -pi/2 through pi/2. Special cases:
- If the argument is NaN or its absolute value is greater than 1, then the result is NaN.
- If the argument is zero, then the result is a zero with thesame sign as the argument.
The computed result must be within 1 ulp of the exact result.Results must be semi-monotonic.
atan#
Usage: atan(«NUMBER»)(Implemented in cc.d3web.expression.eval.UnaryMathFunction)
NUMBER -> NUMBER
Returns the arc tangent of a value; the returned angle is in therange -pi/2 through pi/2. Special cases:
- If the argument is NaN, then the result is NaN.
- If the argument is zero, then the result is a zero with thesame sign as the argument.
The computed result must be within 1 ulp of the exact result.Results must be semi-monotonic.
average#
Usage: average(«HISTORY or PRIMITIVE», «[PRIMITIVE]*»)(Implemented in cc.d3web.expression.eval.MinMaxFunction)
HISTORY_NUMBER -> NUMBER HISTORY_DURATION -> DURATION HISTORY_DATE -> DATE HISTORY_BOOLEAN -> BOOLEAN
NUMBER x NUMBER -> NUMBER DURATION x DURATION -> DURATION DATE x DATE -> DATE BOOLEAN x BOOLEAN -> BOOLEAN
NUMBER x NUMBER x NUMBER -> NUMBER DURATION x DURATION x DURATION -> DURATION DATE x DATE x DATE -> DATE BOOLEAN x BOOLEAN x BOOLEAN -> BOOLEAN
NUMBER x NUMBER x NUMBER x NUMBER -> NUMBER DURATION x DURATION x DURATION x DURATION -> DURATION DATE x DATE x DATE x DATE -> DATE BOOLEAN x BOOLEAN x BOOLEAN x BOOLEAN -> BOOLEAN
Returns the average (mean) value of the one argument history or the set of the argument values. Invalid values in history or arguments are ignored. A minimum is returned as long as there is at least one valid value in history or arguments.
cbrt#
Usage: cbrt(«NUMBER»)(Implemented in cc.d3web.expression.eval.UnaryMathFunction)
NUMBER -> NUMBER
Returns the cube root of a double value. For positive finite x, cbrt(-x) == -cbrt(x); that is, the cube root of a negative value is the negative of the cube root of that value's magnitude. Special cases:
- If the argument is NaN, then the result is NaN.
- If the argument is infinite, then the result is an infinity with the same sign as the argument.
- If the argument is zero, then the result is a zero with the same sign as the argument.
The computed result must be within 1 ulp of the exact result.
ceil#
Usage: ceil(«NUMBER»)(Implemented in cc.d3web.expression.eval.UnaryMathFunction)
NUMBER -> NUMBER
Returns the smallest (closest to negative infinity) double value that is greater than or equal to the argument and is equal to a mathematical integer. Special cases:
- If the argument value is already equal to a mathematical integer, then the result is the same as the argument.
- If the argument is NaN or an infinity or positive zero or negative zero, then the result is the same as the argument.
- If the argument value is less than zero but greater than -1.0, then the result is negative zero. Note that the value of Math.ceil(x) is exactly the value of -Math.floor(-x).
cos#
Usage: cos(«NUMBER»)(Implemented in cc.d3web.expression.eval.UnaryMathFunction)
NUMBER -> NUMBER
Returns the trigonometric cosine of an angle. Special cases:
- If the argument is NaN or an infinity, then the result is NaN.
The computed result must be within 1 ulp of the exact result.Results must be semi-monotonic.
cosh#
Usage: cosh(«NUMBER»)(Implemented in cc.d3web.expression.eval.UnaryMathFunction)
NUMBER -> NUMBER
Returns the hyperbolic cosine of a double value. The hyperbolic cosine of x is defined to be (e x + e -x )/2 where e is Euler's number.
Special cases:
- If the argument is NaN, then the result is NaN.
- If the argument is infinite, then the result is positive infinity.
- If the argument is zero, then the result is 1.0.
The computed result must be within 2.5 ulps of the exact result.
count#
Usage: count(«HISTORY»)(Implemented in cc.d3web.expression.eval.CountFunction)
HISTORY_BOOLEAN -> NUMBER HISTORY_DATE -> NUMBER HISTORY_DURATION -> NUMBER HISTORY_NUMBER -> NUMBER HISTORY_STRING -> NUMBER
Returns the number of entries of the argument history. It is not taken into consideration whether the entry's values are valid or not.
date#
Usage: date(«YEAR», «MONTH», «DAY»)(Implemented in cc.d3web.expression.eval.DateFunction)
NUMBER x NUMBER x NUMBER -> DATE
Creates a new date with the specified YEAR, MONTH and DAY. The argument MONTH must be between 1 and 12, and the DAY between 1 and the total days of the specific month. If any of the arguments is undefined, the function also returns undefined.
dayOfMonth#
Usage: dayOfMonth(«DATE»)(Implemented in cc.d3web.expression.eval.DateFunction)
DATE -> NUMBER
Returns the day within the month specified by the given date, a value between 1 to 31 (or 30, 28, 29 respectively).
dayOfWeek#
Usage: dayOfWeek(«DATE»)(Implemented in cc.d3web.expression.eval.DateFunction)
DATE -> NUMBER
Returns the day of week of the specified date as integer representation. That is, Sunday = 1, Monday = 2... Saturday = 7.
daysOfMonth#
Usage: daysOfMonth(«DATE»)(Implemented in cc.d3web.expression.eval.DateFunction)
DATE -> NUMBER
Returns the last day of the month that contains the specified date, so it is either 28 or 29 for february or 30 or 31 for all other months. Be careful not to mix it up with 'dayOfMonth' which returns the day of the specified date, instead of the month's last day.
delta#
Usage: delta(«HISTORY or PRIMITIVE», «[PRIMITIVE]*»)(Implemented in cc.d3web.expression.eval.MinMaxFunction)
HISTORY_NUMBER -> NUMBER HISTORY_DURATION -> DURATION HISTORY_DATE -> DATE HISTORY_BOOLEAN -> BOOLEAN
NUMBER x NUMBER -> NUMBER DURATION x DURATION -> DURATION DATE x DATE -> DATE BOOLEAN x BOOLEAN -> BOOLEAN
NUMBER x NUMBER x NUMBER -> NUMBER DURATION x DURATION x DURATION -> DURATION DATE x DATE x DATE -> DATE BOOLEAN x BOOLEAN x BOOLEAN -> BOOLEAN
NUMBER x NUMBER x NUMBER x NUMBER -> NUMBER DURATION x DURATION x DURATION x DURATION -> DURATION DATE x DATE x DATE x DATE -> DATE BOOLEAN x BOOLEAN x BOOLEAN x BOOLEAN -> BOOLEAN
Returns the difference between the maximum value and the minimum value of the one argument history or the set of the argument values. Invalid values in history or arguments are ignored. A delta is returned as long as there are at least two valid values in history or arguments.
div#
Usage: div(«ARGUMENT», «ARGUMENT»)(Implemented in cc.d3web.expression.eval.NumberOperator)
NUMBER x NUMBER -> NUMBER DURATION x NUMBER -> DURATION DURATION x DURATION -> NUMBER
Returns the ratio of the two arguments. The result is always a floating pointed value.You may also use the inline operator '/'
duration#
Usage: duration(«HISTORY»)(Implemented in cc.d3web.expression.eval.CountFunction)
HISTORY_BOOLEAN -> DURATION HISTORY_DATE -> DURATION HISTORY_DURATION -> DURATION HISTORY_NUMBER -> DURATION HISTORY_STRING -> DURATION
Returns the total duration of all entries of the argument history. It is not taken into consideration whether the entry's values are valid or not. If the time span of a history entry exceeds the time span of the history only the time span within the history's time span is considered.
equal#
Usage: equal(«ARGUMENT», «ARGUMENT»)(Implemented in cc.d3web.expression.eval.LogicalOperator)
BOOLEAN x BOOLEAN -> BOOLEAN HISTORY_BOOLEAN x BOOLEAN -> BOOLEAN BOOLEAN x HISTORY_BOOLEAN -> BOOLEAN STRING x STRING -> BOOLEAN HISTORY_STRING x STRING -> BOOLEAN STRING x HISTORY_STRING -> BOOLEAN DURATION x DURATION -> BOOLEAN HISTORY_DURATION x DURATION -> BOOLEAN DURATION x HISTORY_DURATION -> BOOLEAN DATE x DATE -> BOOLEAN HISTORY_DATE x DATE -> BOOLEAN DATE x HISTORY_DATE -> BOOLEAN NUMBER x NUMBER -> BOOLEAN HISTORY_NUMBER x NUMBER -> BOOLEAN NUMBER x HISTORY_NUMBER -> BOOLEAN
Returns true, if both argument are equal, false otherwise. Instead of the function you can also use the inline operator '='. If one of the specified arguments is a history, it returns true if all defined values of the history holds the condition. Undefined values of the history will be ignored. If the history is empty or only contains undefined values, the method returns undefined.
exp#
Usage: exp(«NUMBER»)(Implemented in cc.d3web.expression.eval.UnaryMathFunction)
NUMBER -> NUMBER
Returns Euler's number e raised to the power of adouble value. Special cases:
- If the argument is NaN, the result is NaN.
- If the argument is positive infinity, then the result is positive infinity.
- If the argument is negative infinity, then the result is positive zero.
The computed result must be within 1 ulp of the exact result.Results must be semi-monotonic.
expm1#
Usage: expm1(«NUMBER»)(Implemented in cc.d3web.expression.eval.UnaryMathFunction)
NUMBER -> NUMBER
Returns e x -1. Note that for values ofx near 0, the exact sum of expm1(x) + 1 is much closer to the true result of e x than exp(x).
Special cases:
- If the argument is NaN, the result is NaN.
- If the argument is positive infinity, then the result is positive infinity.
- If the argument is negative infinity, then the result is -1.0.
- If the argument is zero, then the result is a zero with the same sign as the argument.
The computed result must be within 1 ulp of the exact result. Results must be semi-monotonic. The result of expm1 for any finite input must be greater than or equal to -1.0. Note that once the exact result of e x - 1 is within 1/2 ulp of the limit value -1, -1.0 should be returned.
filter#
Usage: filter(«HISTORY», «[OPERATOR]», «VALUE»)(Implemented in cc.d3web.expression.eval.FilterFunction)
HISTORY_BOOLEAN x BOOLEAN -> HISTORY_BOOLEAN HISTORY_DATE x DATE -> HISTORY_DATE HISTORY_DURATION x DURATION -> HISTORY_DURATION HISTORY_NUMBER x NUMBER -> HISTORY_NUMBER HISTORY_STRING x STRING -> HISTORY_STRING
HISTORY_BOOLEAN x STRING x BOOLEAN -> HISTORY_BOOLEAN HISTORY_DATE x STRING x DATE -> HISTORY_DATE HISTORY_DURATION x STRING x DURATION -> HISTORY_DURATION HISTORY_NUMBER x STRING x NUMBER -> HISTORY_NUMBER HISTORY_STRING x STRING x STRING -> HISTORY_STRING
Returns a new history with all the values of the given history that do not satisfy the given value or condition (combination of operator and value) being removed. In this resulting history there might be time gaps in between the history entries. When accessing values for time stamps in these gaps, undefined is returned as the value. (See also function valueAt).
The type of the specified value must match the type specified history. You may optionally specify a compare operator as a string parameter. If a compare operator is specified it must be one of the following: '<', '<=', '=', '==', '!=', '>=', '>' or alternatively 'lt', 'le', 'eq', 'unequal', 'ge', 'gt'. If an other string is specified as the operator it defaults to '='.
firstChange#
Usage: firstChange(«HISTORY»)(Implemented in cc.d3web.expression.eval.ChangeFunction)
HISTORY_ANY -> DATE
Returns the date when the first value of the specified history has been set. Please note that for sub-histories the time may be before the start time of the sub-history, because the first value has been set before that time (and is still valid at the sub-histories start time). If the specified history is empty, undefined is returned.
floor#
Usage: floor(«NUMBER»)(Implemented in cc.d3web.expression.eval.UnaryMathFunction)
NUMBER -> NUMBER
Returns the largest (closest to positive infinity) double value that is less than or equal to the argument and is equal to a mathematical integer. Special cases:
- If the argument value is already equal to a mathematical integer, then the result is the same as the argument.
- If the argument is NaN or an infinity or positive zero or negative zero, then the result is the same as the argument.
ge#
Usage: ge(«ARGUMENT», «ARGUMENT»)(Implemented in cc.d3web.expression.eval.LogicalOperator)
STRING x STRING -> BOOLEAN HISTORY_STRING x STRING -> BOOLEAN STRING x HISTORY_STRING -> BOOLEAN DURATION x DURATION -> BOOLEAN HISTORY_DURATION x DURATION -> BOOLEAN DURATION x HISTORY_DURATION -> BOOLEAN DATE x DATE -> BOOLEAN HISTORY_DATE x DATE -> BOOLEAN DATE x HISTORY_DATE -> BOOLEAN NUMBER x NUMBER -> BOOLEAN HISTORY_NUMBER x NUMBER -> BOOLEAN NUMBER x HISTORY_NUMBER -> BOOLEAN
Returns true, if the first argument is greater or equal than the second one, false otherwise. Instead of the function you can also use the inline operator '>='. If one of the specified arguments is a history, it returns true if all defined values of the history holds the condition. Undefined values of the history will be ignored. If the history is empty or only contains undefined values, the method returns undefined.
gradient#
Usage: gradient(«NUMBER HISTORY», «[BASE_DURATION]»)(Implemented in cc.d3web.expression.eval.analysis.GradientFunction)
HISTORY_NUMBER -> NUMBER
HISTORY_NUMBER x DURATION -> NUMBER
Returns the total increase of a linear fitted line within the given (sub-)history.
Computes the best fit (least squares) line y = ax + b through the set of points given by the argument history. The slope a is multiplied by the duration between the timestaps of the first and the last element within the specified history. The multiplication result is returned.
As a special case, the gradient is defined as 0.0, if the argument history contains only one element.
If the history has any undefined values, these values are ignored and the gradient of the other values is calculated.
As an optional argument a duration can be specified that is used instead of the the duration between the first and the last history entry (also undefined entries are considered!), to be used for multiplication. Then the result will be the average increase of the histories values per this duration. Note that if the duration is longer than the history, the increase will be forecasted by assuming to remain constant (in average).
gt#
Usage: gt(«ARGUMENT», «ARGUMENT»)(Implemented in cc.d3web.expression.eval.LogicalOperator)
STRING x STRING -> BOOLEAN HISTORY_STRING x STRING -> BOOLEAN STRING x HISTORY_STRING -> BOOLEAN DURATION x DURATION -> BOOLEAN HISTORY_DURATION x DURATION -> BOOLEAN DURATION x HISTORY_DURATION -> BOOLEAN DATE x DATE -> BOOLEAN HISTORY_DATE x DATE -> BOOLEAN DATE x HISTORY_DATE -> BOOLEAN NUMBER x NUMBER -> BOOLEAN HISTORY_NUMBER x NUMBER -> BOOLEAN NUMBER x HISTORY_NUMBER -> BOOLEAN
Returns true, if the first argument is greater than the second one, false otherwise. Instead of the function you can also use the inline operator '>'. If one of the specified arguments is a history, it returns true if all defined values of the history holds the condition. Undefined values of the history will be ignored. If the history is empty or only contains undefined values, the method returns undefined.
hour#
Usage: hour(«DATE»)(Implemented in cc.d3web.expression.eval.DateFunction)
DATE -> NUMBER
Returns the hour of a given date. Here, the 24-hour clock is assumed, i.e. midnight returns 0, noon returns 12, 10 am returns 10, 10pm returns 22, and so on. The returned value is between 0 and 23.
if#
Usage: if(«CONDITION», «THEN», «[ELSE]», «[UNKNOWN]»)(Implemented in cc.d3web.expression.eval.IfFunction)
BOOLEAN x BOOLEAN -> BOOLEAN BOOLEAN x DATE -> DATE BOOLEAN x DURATION -> DURATION BOOLEAN x NUMBER -> NUMBER BOOLEAN x STRING -> STRING
BOOLEAN x BOOLEAN x BOOLEAN -> BOOLEAN BOOLEAN x DATE x DATE -> DATE BOOLEAN x DURATION x DURATION -> DURATION BOOLEAN x NUMBER x NUMBER -> NUMBER BOOLEAN x STRING x STRING -> STRING
BOOLEAN x BOOLEAN x BOOLEAN x BOOLEAN -> BOOLEAN BOOLEAN x DATE x DATE x DATE -> DATE BOOLEAN x DURATION x DURATION x DURATION -> DURATION BOOLEAN x NUMBER x NUMBER x NUMBER -> NUMBER BOOLEAN x STRING x STRING x STRING -> STRING
Checks the first argument as the condition and returns one of the following arguments as the result of the if-function.
If the first argument is 'true', the function call will result to the value of the second argument. If the first argument evaluates to 'false', the function call will result to the value of the third argument. If the first argument cannot be evaluated to a definite value ('unknown'), the function call will result to the value of the fourth argument.
If the condition if false or unknown and there is no third or fourth argument, the if-function evaluates to unknown.
invalidCount#
Usage: invalidCount(«HISTORY»)(Implemented in cc.d3web.expression.eval.CountFunction)
HISTORY_BOOLEAN -> NUMBER HISTORY_DATE -> NUMBER HISTORY_DURATION -> NUMBER HISTORY_NUMBER -> NUMBER HISTORY_STRING -> NUMBER
Returns the number of invalid entries of the argument history. Invalid entries are those entries which do not have a defined value.
invalidDuration#
Usage: invalidDuration(«HISTORY»)(Implemented in cc.d3web.expression.eval.CountFunction)
HISTORY_BOOLEAN -> DURATION HISTORY_DATE -> DURATION HISTORY_DURATION -> DURATION HISTORY_NUMBER -> DURATION HISTORY_STRING -> DURATION
Returns the total duration of the invalid entries of the argument history. Invalid entries are those entries which do not have a defined value. If the time span of a history entry exceeds the time spand of the history only the time span within the history's time span is considered.
invalidDurationRatio#
Usage: invalidDurationRatio(«HISTORY»)(Implemented in cc.d3web.expression.eval.CountFunction)
HISTORY_BOOLEAN -> NUMBER HISTORY_DATE -> NUMBER HISTORY_DURATION -> NUMBER HISTORY_NUMBER -> NUMBER HISTORY_STRING -> NUMBER
Returns the ratio of invalid entrys' durations of the argument history compared to the total duration of all its entries. If the history has no entires at all, '0' is returned to reflect that there are no invalid entries within the history. If the time span of a history entry exceeds the time spand of the history only the time span within the history's time span is considered.
invalidRatio#
Usage: invalidRatio(«HISTORY»)(Implemented in cc.d3web.expression.eval.CountFunction)
HISTORY_BOOLEAN -> NUMBER HISTORY_DATE -> NUMBER HISTORY_DURATION -> NUMBER HISTORY_NUMBER -> NUMBER HISTORY_STRING -> NUMBER
Returns the ratio of invalid entries of the argument history compared to the number of its total entries. If the history has no entires at all, '0' is returned to reflect that there are no invalid entries within the history.
isNewer#
Usage: isNewer(«HISTORY1», «HISTORY2»)(Implemented in cc.d3web.expression.eval.ChangeFunction)
HISTORY_ANY x HISTORY_ANY -> BOOLEAN
Returns 'lastChange' of the first history is newer as the 'lastChange' time of the second history. It returns false if both have been updated at the same time. If any of the specified histories are empty, undefined is returned.
known#
Usage: known(«QUESTION»)(Implemented in cc.d3web.expression.eval.KnownFunction)
BOOLEAN -> BOOLEAN DATE -> BOOLEAN DURATION -> BOOLEAN NUMBER -> BOOLEAN STRING -> BOOLEAN
Checks if the specified value is valid (known). It is usually used when accessing question values to check if the value has a known and defined value. If a question is not answered or answered by 'unknown' false is returned, true otherwise.
latestChange#
Usage: latestChange(«HISTORY»)(Implemented in cc.d3web.expression.eval.ChangeFunction)
HISTORY_ANY -> DATE
Returns the date when the most recent value of the specified history has been set. If the specified history is empty, undefined is returned.
latestValue#
Usage: latestValue(«HISTORY1», «[HISTORY2]», «[HISTORY3]»)(Implemented in cc.d3web.expression.eval.ChangeFunction)
HISTORY_BOOLEAN -> BOOLEAN HISTORY_DATE -> DATE HISTORY_DURATION -> DURATION HISTORY_NUMBER -> NUMBER HISTORY_STRING -> STRING
HISTORY_BOOLEAN x HISTORY_BOOLEAN -> BOOLEAN HISTORY_DATE x HISTORY_DATE -> DATE HISTORY_DURATION x HISTORY_DURATION -> DURATION HISTORY_NUMBER x HISTORY_NUMBER -> NUMBER HISTORY_STRING x HISTORY_STRING -> STRING
HISTORY_BOOLEAN x HISTORY_BOOLEAN x HISTORY_BOOLEAN -> BOOLEAN HISTORY_DATE x HISTORY_DATE x HISTORY_DATE -> DATE HISTORY_DURATION x HISTORY_DURATION x HISTORY_DURATION -> DURATION HISTORY_NUMBER x HISTORY_NUMBER x HISTORY_NUMBER -> NUMBER HISTORY_STRING x HISTORY_STRING x HISTORY_STRING -> STRING
Returns the most recent value stored in the specified history or histories. If two histories have values with the same most recent start timestamp, the value of the first specified history is returned. If any of the specified histories is empty, it is ignored. If all specified histories are empty, undefined is returned.
le#
Usage: le(«ARGUMENT», «ARGUMENT»)(Implemented in cc.d3web.expression.eval.LogicalOperator)
STRING x STRING -> BOOLEAN HISTORY_STRING x STRING -> BOOLEAN STRING x HISTORY_STRING -> BOOLEAN DURATION x DURATION -> BOOLEAN HISTORY_DURATION x DURATION -> BOOLEAN DURATION x HISTORY_DURATION -> BOOLEAN DATE x DATE -> BOOLEAN HISTORY_DATE x DATE -> BOOLEAN DATE x HISTORY_DATE -> BOOLEAN NUMBER x NUMBER -> BOOLEAN HISTORY_NUMBER x NUMBER -> BOOLEAN NUMBER x HISTORY_NUMBER -> BOOLEAN
Returns true, if the first argument is less or equal than the second one, false otherwise. Instead of the function you can also use the inline operator '<='. If one of the specified arguments is a history, it returns true if all defined values of the history holds the condition. Undefined values of the history will be ignored. If the history is empty or only contains undefined values, the method returns undefined.
log#
Usage: log(«NUMBER»)(Implemented in cc.d3web.expression.eval.UnaryMathFunction)
NUMBER -> NUMBER
Returns the natural logarithm (base e) of a double value. Special cases:
- If the argument is NaN or less than zero, then the result is NaN.
- If the argument is positive infinity, then the result is positive infinity.
- If the argument is positive zero or negative zero, then the result is negative infinity.
The computed result must be within 1 ulp of the exact result. Results must be semi-monotonic.
log10#
Usage: log10(«NUMBER»)(Implemented in cc.d3web.expression.eval.UnaryMathFunction)
NUMBER -> NUMBER
Returns the base 10 logarithm of a double value. Special cases:
- If the argument is NaN or less than zero, then the result is NaN.
- If the argument is positive infinity, then the result is positive infinity.
- If the argument is positive zero or negative zero, then the result is negative infinity.
- If the argument is equal to 10 n for integer n, then the result is n.
The computed result must be within 1 ulp of the exact result. Results must be semi-monotonic.
log1p#
Usage: log1p(«NUMBER»)(Implemented in cc.d3web.expression.eval.UnaryMathFunction)
NUMBER -> NUMBER
Returns the natural logarithm of the sum of the argument and 1. Note that for small values x, the result of log1p(x) is much closer to the true result of ln(1 + x) than the floating-point evaluation of log(1.0+x).
Special cases:
- If the argument is NaN or less than -1, then the result is NaN.
- If the argument is positive infinity, then the result is positive infinity.
- If the argument is negative one, then the result is negative infinity.
- If the argument is zero, then the result is a zero with the same sign as the argument.
The computed result must be within 1 ulp of the exact result. Results must be semi-monotonic.
lt#
Usage: lt(«ARGUMENT», «ARGUMENT»)(Implemented in cc.d3web.expression.eval.LogicalOperator)
STRING x STRING -> BOOLEAN HISTORY_STRING x STRING -> BOOLEAN STRING x HISTORY_STRING -> BOOLEAN DURATION x DURATION -> BOOLEAN HISTORY_DURATION x DURATION -> BOOLEAN DURATION x HISTORY_DURATION -> BOOLEAN DATE x DATE -> BOOLEAN HISTORY_DATE x DATE -> BOOLEAN DATE x HISTORY_DATE -> BOOLEAN NUMBER x NUMBER -> BOOLEAN HISTORY_NUMBER x NUMBER -> BOOLEAN NUMBER x HISTORY_NUMBER -> BOOLEAN
Returns true, if the first argument is less than the second one, false otherwise. Instead of the function you can also use the inline operator '<'. If one of the specified arguments is a history, it returns true if all defined values of the history holds the condition. Undefined values of the history will be ignored. If the history is empty or only contains undefined values, the method returns undefined.
max#
Usage: max(«HISTORY or PRIMITIVE», «[PRIMITIVE]*»)(Implemented in cc.d3web.expression.eval.MinMaxFunction)
HISTORY_NUMBER -> NUMBER HISTORY_DURATION -> DURATION HISTORY_DATE -> DATE HISTORY_BOOLEAN -> BOOLEAN HISTORY_STRING -> STRING
NUMBER x NUMBER -> NUMBER DURATION x DURATION -> DURATION DATE x DATE -> DATE BOOLEAN x BOOLEAN -> BOOLEAN STRING x STRING -> STRING
NUMBER x NUMBER x NUMBER -> NUMBER DURATION x DURATION x DURATION -> DURATION DATE x DATE x DATE -> DATE BOOLEAN x BOOLEAN x BOOLEAN -> BOOLEAN STRING x STRING x STRING -> STRING
NUMBER x NUMBER x NUMBER x NUMBER -> NUMBER DURATION x DURATION x DURATION x DURATION -> DURATION DATE x DATE x DATE x DATE -> DATE BOOLEAN x BOOLEAN x BOOLEAN x BOOLEAN -> BOOLEAN STRING x STRING x STRING x STRING -> STRING
Returns the maximum value of the one argument history or the set of the argument values. Invalid values in history or arguments are ignored. A maximum is returned as long as there is at least one valid value in history or arguments.
median#
Usage: median(«HISTORY»)(Implemented in cc.d3web.expression.eval.analysis.MedianFunction)
HISTORY_NUMBER -> NUMBER
This is an implementation of the median function. It searches the median of the {@link HistoryEntry}s within the specified numeric history (HISTORY_NUMBER).
If the number of entries to the history is even, the lower median is returned. It is guaranteed that the returned median is always an existing entry of the history. This allows the function also to be used e.g. for choice values. The duration of the history entries is not taken into consideration. Therefore the values are not 'weighted' by the time they has been valid. If the history has any undefined values, these values are ignored and the median of the other values is calculated.
The function returns either the non-null median element of the history or null if (and only if) there are no non-null values within the history.
min#
Usage: min(«HISTORY or PRIMITIVE», «[PRIMITIVE]*»)(Implemented in cc.d3web.expression.eval.MinMaxFunction)
HISTORY_NUMBER -> NUMBER HISTORY_DURATION -> DURATION HISTORY_DATE -> DATE HISTORY_BOOLEAN -> BOOLEAN HISTORY_STRING -> STRING
NUMBER x NUMBER -> NUMBER DURATION x DURATION -> DURATION DATE x DATE -> DATE BOOLEAN x BOOLEAN -> BOOLEAN STRING x STRING -> STRING
NUMBER x NUMBER x NUMBER -> NUMBER DURATION x DURATION x DURATION -> DURATION DATE x DATE x DATE -> DATE BOOLEAN x BOOLEAN x BOOLEAN -> BOOLEAN STRING x STRING x STRING -> STRING
NUMBER x NUMBER x NUMBER x NUMBER -> NUMBER DURATION x DURATION x DURATION x DURATION -> DURATION DATE x DATE x DATE x DATE -> DATE BOOLEAN x BOOLEAN x BOOLEAN x BOOLEAN -> BOOLEAN STRING x STRING x STRING x STRING -> STRING
Returns the minimum value of the one argument history or the set of the argument values. Invalid values in history or arguments are ignored. A minimum is returned as long as there is at least one valid value in history or arguments.
minus#
Usage: minus(«ARGUMENT», «ARGUMENT»)(Implemented in cc.d3web.expression.eval.NumberOperator)
NUMBER x NUMBER -> NUMBER DATE x DURATION -> DATE DATE x DATE -> DURATION DURATION x DURATION -> DURATION
Returns the difference of the two arguments. You may also use the inline operator '-'
minute#
Usage: minute(«DATE»)(Implemented in cc.d3web.expression.eval.DateFunction)
DATE -> NUMBER
Returns the minute of a given date, from 0 to 59.
mod#
Usage: mod(«ARGUMENT», «ARGUMENT»)(Implemented in cc.d3web.expression.eval.NumberOperator)
NUMBER x NUMBER -> NUMBER DURATION x DURATION -> DURATION
Returns the remainder of the of the two arguments. The remainder is the rest when calculating the integer-ratio of both. You may also use the inline operator '%'
month#
Usage: month(«DATE»)(Implemented in cc.d3web.expression.eval.DateFunction)
DATE -> NUMBER
Returns the month as a number for a given date, i.e. 1 for January, 2 for February, and so on.
mult#
Usage: mult(«ARGUMENT», «ARGUMENT»)(Implemented in cc.d3web.expression.eval.NumberOperator)
NUMBER x NUMBER -> NUMBER DURATION x NUMBER -> DURATION NUMBER x DURATION -> DURATION
Returns the product of the two arguments. You may also use the inline operator '*'
neg#
Usage: neg(«NUMBER»)(Implemented in cc.d3web.expression.eval.UnaryMathFunction)
NUMBER -> NUMBER DURATION -> DURATION
Returns the negated value of the argument.
not#
Usage: not(«BOOLEAN»)(Implemented in cc.d3web.expression.eval.LogicalOperator)
BOOLEAN -> BOOLEAN
Returns true, if the argument is false, and vica verse. Instead of the function you can also use the inline operator '!'.
or#
Usage: or(«BOOLEAN», «BOOLEAN»)(Implemented in cc.d3web.expression.eval.LogicalOperator)
BOOLEAN x BOOLEAN -> BOOLEAN
Returns true, if one argument is true. Returns false, if both arguments are false. Otherwise it returns undefined. Instead of the function you can also use the inline operator '|'.
percentEqual#
Usage: percentEqual(«HISTORY», «VALUE»)(Implemented in cc.d3web.expression.eval.CorridorFunction)
HISTORY_BOOLEAN x BOOLEAN -> NUMBER HISTORY_STRING x STRING -> NUMBER HISTORY_DURATION x DURATION -> NUMBER HISTORY_DATE x DATE -> NUMBER HISTORY_NUMBER x NUMBER -> NUMBER
Returns the percentage (between 0 - 1) of the time the specified history has been equal to the specified value. Time periods of undefined values are ignored. If there is no valid value in the history undefined is returned.
percentGe#
Usage: percentGe(«HISTORY», «LIMIT»)(Implemented in cc.d3web.expression.eval.CorridorFunction)
HISTORY_STRING x STRING -> NUMBER HISTORY_DURATION x DURATION -> NUMBER HISTORY_DATE x DATE -> NUMBER HISTORY_NUMBER x NUMBER -> NUMBER
Returns the percentage (between 0 - 1) of the time the specified history has been greater or equal than the specified value. Time periods of undefined values are ignored. If there is no valid value in the history undefined is returned.
percentGt#
Usage: percentGt(«HISTORY», «LIMIT»)(Implemented in cc.d3web.expression.eval.CorridorFunction)
HISTORY_STRING x STRING -> NUMBER HISTORY_DURATION x DURATION -> NUMBER HISTORY_DATE x DATE -> NUMBER HISTORY_NUMBER x NUMBER -> NUMBER
Returns the percentage (between 0 - 1) of the time the specified history has been less than the specified value. Time periods of undefined values are ignored. If there is no valid value in the history undefined is returned.
percentIn#
Usage: percentIn(«HISTORY», «MIN», «MAX»)(Implemented in cc.d3web.expression.eval.CorridorFunction)
HISTORY_STRING x STRING x STRING -> NUMBER HISTORY_DURATION x DURATION x DURATION -> NUMBER HISTORY_DATE x DATE x DATE -> NUMBER HISTORY_NUMBER x NUMBER x NUMBER -> NUMBER
Returns the percentage (between 0 - 1) of the time the specified history has been in between the specified min and max value (limits included). Time periods of undefined values are ignored. If there is no valid value in the history undefined is returned.
percentLe#
Usage: percentLe(«HISTORY», «LIMIT»)(Implemented in cc.d3web.expression.eval.CorridorFunction)
HISTORY_STRING x STRING -> NUMBER HISTORY_DURATION x DURATION -> NUMBER HISTORY_DATE x DATE -> NUMBER HISTORY_NUMBER x NUMBER -> NUMBER
Returns the percentage (between 0 - 1) of the time the specified history has been less or equal than the specified value. Time periods of undefined values are ignored. If there is no valid value in the history undefined is returned.
percentLt#
Usage: percentLt(«HISTORY», «LIMIT»)(Implemented in cc.d3web.expression.eval.CorridorFunction)
HISTORY_STRING x STRING -> NUMBER HISTORY_DURATION x DURATION -> NUMBER HISTORY_DATE x DATE -> NUMBER HISTORY_NUMBER x NUMBER -> NUMBER
Returns the percentage (between 0 - 1) of the time the specified history has been greater than the specified value. Time periods of undefined values are ignored. If there is no valid value in the history undefined is returned.
percentUnequal#
Usage: percentUnequal(«HISTORY», «VALUE»)(Implemented in cc.d3web.expression.eval.CorridorFunction)
HISTORY_BOOLEAN x BOOLEAN -> NUMBER HISTORY_STRING x STRING -> NUMBER HISTORY_DURATION x DURATION -> NUMBER HISTORY_DATE x DATE -> NUMBER HISTORY_NUMBER x NUMBER -> NUMBER
Returns the percentage (between 0 - 1) of the time the specified history has been different to the specified value. Time periods of undefined values are ignored. If there is no valid value in the history undefined is returned.
plus#
Usage: plus(«ARGUMENT», «ARGUMENT»)(Implemented in cc.d3web.expression.eval.NumberOperator)
NUMBER x NUMBER -> NUMBER DURATION x DURATION -> DURATION DATE x DURATION -> DATE DURATION x DATE -> DATE STRING x ANY -> STRING ANY x STRING -> STRING
Returns the sum of the two arguments. You may also use the inline operator '+'
pow#
Usage: pow(«ARGUMENT», «ARGUMENT»)(Implemented in cc.d3web.expression.eval.NumberOperator)
NUMBER x NUMBER -> NUMBER
Returns the value of the first argument raised to the power of the second argument. You may also use the inline operator '^'.
Special cases:
- If the second argument is positive or negative zero, then the result is 1.0.
- If the second argument is 1.0, then the result is the same as the first argument.
- If the second argument is NaN, then the result is NaN.
- If the first argument is NaN and the second argument is nonzero, then the result is NaN.
- If the absolute value of the first argument is greater than 1 and the second argument is positive infinity, then the result is positive infinity.
- If the absolute value of the first argument is less than 1 and the second argument is negative infinity, then the result is positive infinity.
- If the absolute value of the first argument is greater than 1 and the second argument is negative infinity, then the result is positive zero.
- If the absolute value of the first argument is less than 1 and the second argument is positive infinity, then the result is positive zero.
- If the absolute value of the first argument equals 1 and the second argument is infinite, then the result is NaN.
- If the first argument is positive zero and the second argument is greater than zero, or then the result is positive zero.
- If the first argument is positive infinity and the second argument is less than zero, then the result is positive zero.
- If the first argument is positive zero and the second argument is less than zero, then the result is positive infinity.
- If the first argument is positive infinity and the second argument is greater than zero, then the result is positive infinity.
- If the first argument is negative zero and the second argument is greater than zero but not a finite odd integer, then the result is positive zero.
- If the first argument is negative infinity and the second argument is less than zero but not a finite odd integer, then the result is positive zero.
- If the first argument is negative zero and the second argument is a positive finite odd integer, then the result is negative zero.
- If the first argument is negative infinity and the second argument is a negative finite odd integer, then the result is negative zero.
- If the first argument is negative zero and the second argument is less than zero but not a finite odd integer, then the result is positive infinity.
- If the first argument is negative infinity and the second argument is greater than zero but not a finite odd integer, then the result is positive infinity.
- If the first argument is negative zero and the second argument is a negative finite odd integer, then the result is negative infinity.
- If the first argument is negative infinity and the second argument is a positive finite odd integer, then the result is negative infinity.
- If the first argument is finite and less than zero and if the second argument is a finite even integer, the result is equal to the result of raising the absolute value of the first argument to the power of the second argument the result is NaN.
- If the first argument is finite and less than zero and if the second argument is a finite odd integer, the result is equal to the negative of the result of raising the absolute value of the first argument to the power of the second argument the result is NaN.
- If the first argument is finite and less than zero and if the second argument is finite and not an integer, then argument the result is NaN.
- If both arguments are integers, then the result is exactly equal to the mathematical result of raising the first argument to the power of the second argument if that result can in fact be represented exactly as a double value.
(In the foregoing descriptions, a floating-point value is considered to be an integer if and only if it is finite and a fixed point of the method {@link #ceil <tt>ceil</tt>} or, equivalently, a fixed point of the method {@link #floor <tt>floor</tt>}. A value is a fixed point of a one-argument method if and only if the result of applying the method to the value is equal to the value.)
The computed result must be within 1 ulp of the exact result. Results must be semi-monotonic.
rint#
Usage: rint(«NUMBER»)(Implemented in cc.d3web.expression.eval.UnaryMathFunction)
NUMBER -> NUMBER
Returns the double value that is closest in value to the argument and is equal to a mathematical integer. If two double values that are mathematical integers are equally close, the result is the integer value that is even. Special cases:
- If the argument value is already equal to a mathematical integer, then the result is the same as the argument.
- If the argument is NaN or an infinity or positive zero or negative zero, then the result is the same as the argument.
round#
Usage: round(«NUMBER»)(Implemented in cc.d3web.expression.eval.UnaryMathFunction)
NUMBER -> NUMBER
Returns the closest int to the argument. The result is rounded to an integer by adding 1/2, taking the floor of the result, and casting the result to type int. In other words, the result is equal to the value of the expression:
(int)Math.floor(a + 0.5f)
Special cases:
- If the argument is NaN, the result is 0.
- If the argument is negative infinity or any value less than or equal to the value of Integer.MIN_VALUE, the result is equal to the value of Integer.MIN_VALUE.
- If the argument is positive infinity or any value greater than or equal to the value of Integer.MAX_VALUE, the result is equal to the value of Integer.MAX_VALUE.
second#
Usage: second(«DATE»)(Implemented in cc.d3web.expression.eval.DateFunction)
DATE -> NUMBER
Returns the second of a given date, from 0 to 59.
signum#
Usage: signum(«NUMBER»)(Implemented in cc.d3web.expression.eval.UnaryMathFunction)
NUMBER -> NUMBER
Returns the signum function of the argument; zero if the argument is zero, 1.0 if the argument is greater than zero, -1.0 if the argument is less than zero.
Special Cases:
- If the argument is NaN, then the result is NaN.
- If the argument is positive zero or negative zero, then the result is the same as the argument.
sin#
Usage: sin(«NUMBER»)(Implemented in cc.d3web.expression.eval.UnaryMathFunction)
NUMBER -> NUMBER
Returns the trigonometric sine of an angle. Special cases:
- If the argument is NaN or an infinity, then the result is NaN.
- If the argument is zero, then the result is a zero with thesame sign as the argument.
The computed result must be within 1 ulp of the exact result.Results must be semi-monotonic.
since#
Usage: since(«HISTORY»)(Implemented in cc.d3web.expression.eval.ChangeFunction)
HISTORY_ANY -> DATE
Returns the date since the value of the specified history remains unchanged. The function therefore ignores any value entries in the history that has not altered the value. If the specified history is empty, undefined is returned.
sinh#
Usage: sinh(«NUMBER»)(Implemented in cc.d3web.expression.eval.UnaryMathFunction)
NUMBER -> NUMBER
Returns the hyperbolic sine of a double value. The hyperbolic sine of x is defined to be (e x - e -x )/2 where e is Euler's number.
Special cases:
- If the argument is NaN, then the result is NaN.
- If the argument is infinite, then the result is an infinity with the same sign as the argument.
- If the argument is zero, then the result is a zero with the same sign as the argument.
The computed result must be within 2.5 ulps of the exact result.
sqrt#
Usage: sqrt(«NUMBER»)(Implemented in cc.d3web.expression.eval.UnaryMathFunction)
NUMBER -> NUMBER
Returns the correctly rounded positive square root of a double value. Special cases:
- If the argument is NaN or less than zero, then the result is NaN.
- If the argument is positive infinity, then the result is positive infinity.
- If the argument is positive zero or negative zero, then the result is the same as the argument.
strictSubHistory#
Usage: strictSubHistory(«HISTORY», «START», «END»)(Implemented in cc.d3web.expression.eval.StrictSubHistoryFunction)
HISTORY_BOOLEAN x DATE x DATE -> HISTORY_BOOLEAN HISTORY_DATE x DATE x DATE -> HISTORY_DATE HISTORY_DURATION x DATE x DATE -> HISTORY_DURATION HISTORY_NUMBER x DATE x DATE -> HISTORY_NUMBER HISTORY_STRING x DATE x DATE -> HISTORY_STRING HISTORY_BOOLEAN x DURATION x DURATION -> HISTORY_BOOLEAN HISTORY_DATE x DURATION x DURATION -> HISTORY_DATE HISTORY_DURATION x DURATION x DURATION -> HISTORY_DURATION HISTORY_NUMBER x DURATION x DURATION -> HISTORY_NUMBER HISTORY_STRING x DURATION x DURATION -> HISTORY_STRING
Access a sub-history in a certain time range. There is no special order of the 'START' or 'END' parameters required, the sub-history starts at the earlier time point an lasts to the later one. If the history has no values within the specified time range, an empty history is returned. If the requested sub-history starts before the history it is taken from, the start time is the latter one. Please note that only history entries at or after the requested start time will be used as the result of the strict-sub-history. This is the difference to the 'subHistory' function.
If you specify a duration instead of a time for the 'START' or 'END' parameter, the time to be used is calculated relatively to the history's last entry. Regardless whether the value is positive or negative, the used date is the specified time before the history's end. Due to avoid confusion, it is not allowed to mix date and duration as arguments.
Examples:
- my_history[0min, 5min]: results to the last 5 minutes of the variable my_history since the last recorded change of the xps session.
- my_history[0min, -5min]: also results to the last 5 minutes of the xps session. It is identical to the example above.
- my_history[now, now-5min]: results to the changes of the variable my_history during the last 5 minutes of the xps session. It is identical to the example above.
- my_history[start, start+5min]: results to the changes of the variable my_history during the first 5 minutes of the xps session.
You may also use the inline operator «HISTORY»![«START» , «END»].
subHistory#
Usage: subHistory(«HISTORY», «START», «END»)(Implemented in cc.d3web.expression.eval.SubHistoryFunction)
HISTORY_BOOLEAN x DATE x DATE -> HISTORY_BOOLEAN HISTORY_DATE x DATE x DATE -> HISTORY_DATE HISTORY_DURATION x DATE x DATE -> HISTORY_DURATION HISTORY_NUMBER x DATE x DATE -> HISTORY_NUMBER HISTORY_STRING x DATE x DATE -> HISTORY_STRING HISTORY_BOOLEAN x DURATION x DURATION -> HISTORY_BOOLEAN HISTORY_DATE x DURATION x DURATION -> HISTORY_DATE HISTORY_DURATION x DURATION x DURATION -> HISTORY_DURATION HISTORY_NUMBER x DURATION x DURATION -> HISTORY_NUMBER HISTORY_STRING x DURATION x DURATION -> HISTORY_STRING
Access a sub-history in a certain time range. There is no special order of the 'START' or 'END' parameters required, the sub-history starts at the earlier time point an lasts to the later one. If the history has no values within the specified time range, an empty history is returned. If the requested sub-history starts before the history it is taken from, the start time is the latter one. If the earlier time does not match exactly an existing entry within the history the latest entry before the requested time is used as the first entry of the strict-sub-history.
If you specify a duration instead of a time for the 'START' or 'END' parameter, the time to be used is calculated relatively to the history's last entry. Regardless whether the value is positive or negative, the used date is the specified time before the history's end. Due to avoid confusion, it is not allowed to mix date and duration as arguments.
Examples:
- my_history[0min, 5min]: results to the last 5 minutes of the variable my_history since the last recorded change of the xps session.
- my_history[0min, -5min]: also results to the last 5 minutes of the xps session. It is identical to the example above.
- my_history[now, now-5min]: results to the changes of the variable my_history during the last 5 minutes of the xps session. It is identical to the example above.
- my_history[start, start+5min]: results to the changes of the variable my_history during the first 5 minutes of the xps session.
You may also use the inline operator «HISTORY»[«START» , «END»].
tan#
Usage: tan(«NUMBER»)(Implemented in cc.d3web.expression.eval.UnaryMathFunction)
NUMBER -> NUMBER
Returns the trigonometric tangent of an angle. Special cases:
- If the argument is NaN or an infinity, then the result is NaN.
- If the argument is zero, then the result is a zero with thesame sign as the argument.
The computed result must be within 1 ulp of the exact result.Results must be semi-monotonic.
tanh#
Usage: tanh(«NUMBER»)(Implemented in cc.d3web.expression.eval.UnaryMathFunction)
NUMBER -> NUMBER
Returns the hyperbolic tangent of a double value. The hyperbolic tangent of x is defined to be (e x - e -x )/(e x + e -x ), in other words, sinh(x)/cosh(x). Note that the absolute value of the exact tanh is always less than 1.
Special cases:
- If the argument is NaN, then the result is NaN.
- If the argument is zero, then the result is a zero with the same sign as the argument.
- If the argument is positive infinity, then the result is +1.0.
- If the argument is negative infinity, then the result is -1.0.
The computed result must be within 2.5 ulps of the exact result. The result of tanh for any finite input must have an absolute value less than or equal to 1. Note that once the exact result of tanh is within 1/2 of an ulp of the limit value of ±1, correctly signed ±1.0 should be returned.
toDegrees#
Usage: toDegrees(«NUMBER»)(Implemented in cc.d3web.expression.eval.UnaryMathFunction)
NUMBER -> NUMBER
Converts an angle measured in radians to an approximatelyequivalent angle measured in degrees. The conversion fromradians to degrees is generally inexact; users shouldnot expect cos(toRadians(90.0)) to exactlyequal 0.0.
toRadians#
Usage: toRadians(«NUMBER»)(Implemented in cc.d3web.expression.eval.UnaryMathFunction)
NUMBER -> NUMBER
Converts an angle measured in degrees to an approximatelyequivalent angle measured in radians. The conversion fromdegrees to radians is generally inexact.
unequal#
Usage: unequal(«ARGUMENT», «ARGUMENT»)(Implemented in cc.d3web.expression.eval.LogicalOperator)
BOOLEAN x BOOLEAN -> BOOLEAN HISTORY_BOOLEAN x BOOLEAN -> BOOLEAN BOOLEAN x HISTORY_BOOLEAN -> BOOLEAN STRING x STRING -> BOOLEAN HISTORY_STRING x STRING -> BOOLEAN STRING x HISTORY_STRING -> BOOLEAN DURATION x DURATION -> BOOLEAN HISTORY_DURATION x DURATION -> BOOLEAN DURATION x HISTORY_DURATION -> BOOLEAN DATE x DATE -> BOOLEAN HISTORY_DATE x DATE -> BOOLEAN DATE x HISTORY_DATE -> BOOLEAN NUMBER x NUMBER -> BOOLEAN HISTORY_NUMBER x NUMBER -> BOOLEAN NUMBER x HISTORY_NUMBER -> BOOLEAN
Returns true, if both argument are not equal, false otherwise. Instead of the function you can also use the inline operator '!='. If one of the specified arguments is a history, it returns true if all defined values of the history holds the condition. Undefined values of the history will be ignored. If the history is empty or only contains undefined values, the method returns undefined.
validCount#
Usage: validCount(«HISTORY»)(Implemented in cc.d3web.expression.eval.CountFunction)
HISTORY_BOOLEAN -> NUMBER HISTORY_DATE -> NUMBER HISTORY_DURATION -> NUMBER HISTORY_NUMBER -> NUMBER HISTORY_STRING -> NUMBER
Returns the number of valid entries of the argument history. Valid entries are those entries which have a defined value.
validDuration#
Usage: validDuration(«HISTORY»)(Implemented in cc.d3web.expression.eval.CountFunction)
HISTORY_BOOLEAN -> DURATION HISTORY_DATE -> DURATION HISTORY_DURATION -> DURATION HISTORY_NUMBER -> DURATION HISTORY_STRING -> DURATION
Returns the total duration of the valid entries of the argument history. Valid entries are those entries which have a defined value. If the time span of a history entry exceeds the time spand of the history only the time span within the history's time span is considered.
validDurationRatio#
Usage: validDurationRatio(«HISTORY»)(Implemented in cc.d3web.expression.eval.CountFunction)
HISTORY_BOOLEAN -> NUMBER HISTORY_DATE -> NUMBER HISTORY_DURATION -> NUMBER HISTORY_NUMBER -> NUMBER HISTORY_STRING -> NUMBER
Returns the ratio of valid entrys' durations of the argument history compared to the total duration of all its entries. If the history has no entires at all, '0' is returned to reflect that there are no valid entries within the history. If the time span of a history entry exceeds the time spand of the history only the time span within the history's time span is considered.
validRatio#
Usage: validRatio(«HISTORY»)(Implemented in cc.d3web.expression.eval.CountFunction)
HISTORY_BOOLEAN -> NUMBER HISTORY_DATE -> NUMBER HISTORY_DURATION -> NUMBER HISTORY_NUMBER -> NUMBER HISTORY_STRING -> NUMBER
Returns the ratio of valid entries of the argument history compared to the number of its total entries. If the history has no entires at all, '0' is returned to reflect that there are no valid entries within the history.
valids#
Usage: valids(«HISTORY»)(Implemented in cc.d3web.expression.eval.ValidsFunction)
HISTORY_BOOLEAN -> HISTORY_BOOLEAN HISTORY_DATE -> HISTORY_DATE HISTORY_DURATION -> HISTORY_DURATION HISTORY_NUMBER -> HISTORY_NUMBER HISTORY_STRING -> HISTORY_STRING
Removes all invalid values from the history. This results in a history which only contains the valid values. In this resulting history there might be time gaps in between the history entries. When accessing values for time stamps in these gaps, undefined is returned as the value. (See also function valueAt).
valueAt#
Usage: valueAt(«HISTORY», «TIME»)(Implemented in cc.d3web.expression.eval.ValueAtFunction)
HISTORY_BOOLEAN x DATE -> BOOLEAN HISTORY_DATE x DATE -> DATE HISTORY_DURATION x DATE -> DURATION HISTORY_NUMBER x DATE -> NUMBER HISTORY_STRING x DATE -> STRING HISTORY_BOOLEAN x DURATION -> BOOLEAN HISTORY_DATE x DURATION -> DATE HISTORY_DURATION x DURATION -> DURATION HISTORY_NUMBER x DURATION -> NUMBER HISTORY_STRING x DURATION -> STRING
Access a value of a history to a certain time.If you specify a duration instead of a time for the 'TIME' parameter, the time to be used is calculated relatively to the history's last entry. Regardless whether the duration is positive or negative, the used date is the specified time before the history's end.
Examples:
- my_history[5min]: results to the value of the variable my_history as it has been 5 minutes before the current time of the xps session.
- my_history[-5min]: also results value 5 minutes before the current time of the xps session. It is identical to the example above.
- my_history[now-5min]: results to the value of the variable my_history as it has been 5 minutes before the current time of the xps session.
- my_history[start+5min]: results to the value of the variable my_history as it has been 5 minutes after the xps session has been started.
If you access a value for a specific time of a history, and there is no value available at the exact time, usually the latest value that has been set before the speified time is returned. Only if you create a history with time gaps (e.g. using the functions 'valids' or 'filter'), and ask for values within these time gaps, undefined is returned as the value. To access the latest available value before these gaps, use 'latestChange(«HISTORY»[start, «TIME»])'instead of 'valueAt(«HISTORY», «TIME»)'.
You may also use the inline operator «HISTORY»[«TIME»].
year#
Usage: year(«DATE»)(Implemented in cc.d3web.expression.eval.DateFunction)
DATE -> NUMBER
Returns the year of a given date.

